Classification des Moindres Carrés (Least- Squares Classification)
Classification des Moindres Carrés (Least- Squares Classification)
1 Introduction
La classification consiste à déterminer à quelle catégorie appartient une observation parmi un ensemble de catégories prédéfinies. Ce processus est fondamental dans divers domaines, allant de l’identification du spam dans les e-mails à l’attribution d’un diagnostic à un patient en fonction de ses caractéristiques observées, telles que le sexe, la pression artérielle ou la présence de certains symptômes. Ces observations sont analysées en fonction de caractéristiques quantifiables, pouvant être catégoriques, ordinales, à valeurs entières ou réelles.
Dans l’apprentissage supervisé, les algorithmes de classification utilisent des données étiquetées pour entraîner un modèle. Chaque exemple du jeu de données d’entraînement est associé à une étiquette de classe connue, permettant au modèle d’apprendre à prédire correctement les classes pour de nouvelles observations.
Il existe une multitude d’algorithmes de classification, chacun présentant des caractéristiques distinctes :
-
Classification des moindres carrés (Least-Squares Classification) : Utilise la méthode des moindres carrés pour modéliser les relations linéaires entre les caractéristiques et les étiquettes de classe.
-
Régression Logistique : Utilise une fonction logistique pour estimer les probabilités des classes.
-
Arbres de Décision : Représentent une structure arborescente où chaque nœud représente une caractéristique et les branches déterminent les règles de décision.
-
Machines à Vecteurs de Support (SVM) : Trouvent un hyperplan optimal pour séparer les classes tout en maximisant la marge entre elles.
-
K plus proches voisins (KNN) : Classent les observations en fonction des classes majoritaires parmi les $k$ voisins les plus proches dans l’espace des caractéristiques.
-
Réseaux de Neurones : Modèles complexes apprenant des représentations hiérarchiques des données pour la classification.
Ces algorithmes diffèrent par leurs approches de modélisation et leurs capacités à traiter des structures de données variées. Ils sont sélectionnés en fonction de la nature des données, de la complexité du problème et des performances attendues.
Nous allons nous intéresser plus particulièrement à la méthode de classification des moindres carrés (ou Least-Squares Classification en anglais).
2 Classification des Moindres Carrés (Least-Squares Classification)
Dans la classification des moindres carrés, on s’intéresse à l’utilisation de méthodes de régression pour résoudre des problèmes de classification catégorique.
Prenons le cas d’une classification binaire, où les étiquettes de classe sont -1 ou 1. En utilisant une approche de régression linéaire, on peut former un modèle pour minimiser la somme des carrés des différences entre les prédictions et les étiquettes réelles. Ce modèle peut être représenté comme $y(x) = w^T x$, où $w$ est un vecteur de poids.
La frontière de décision dans la classification des moindres carrés est définie par $w^T x = 0$.
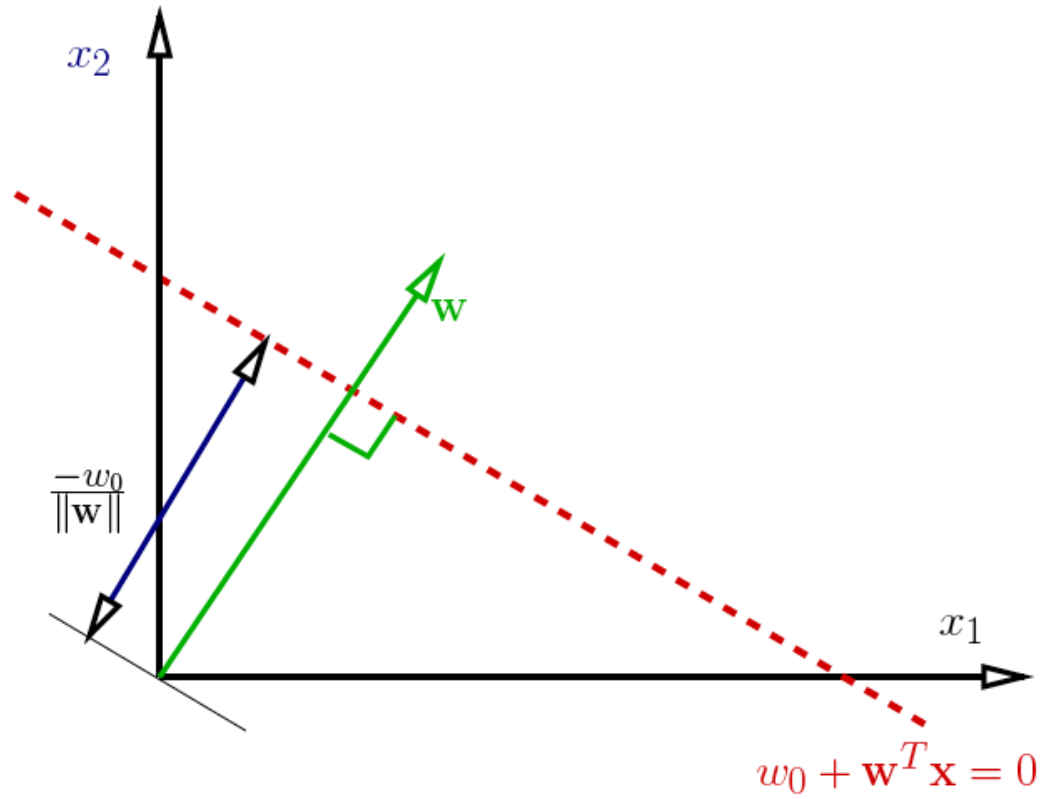
Pour des données en deux dimensions, cette équation représente une ligne droite. En général, dans des espaces de dimensions supérieures, cela forme un hyperplan qui sépare les classes.
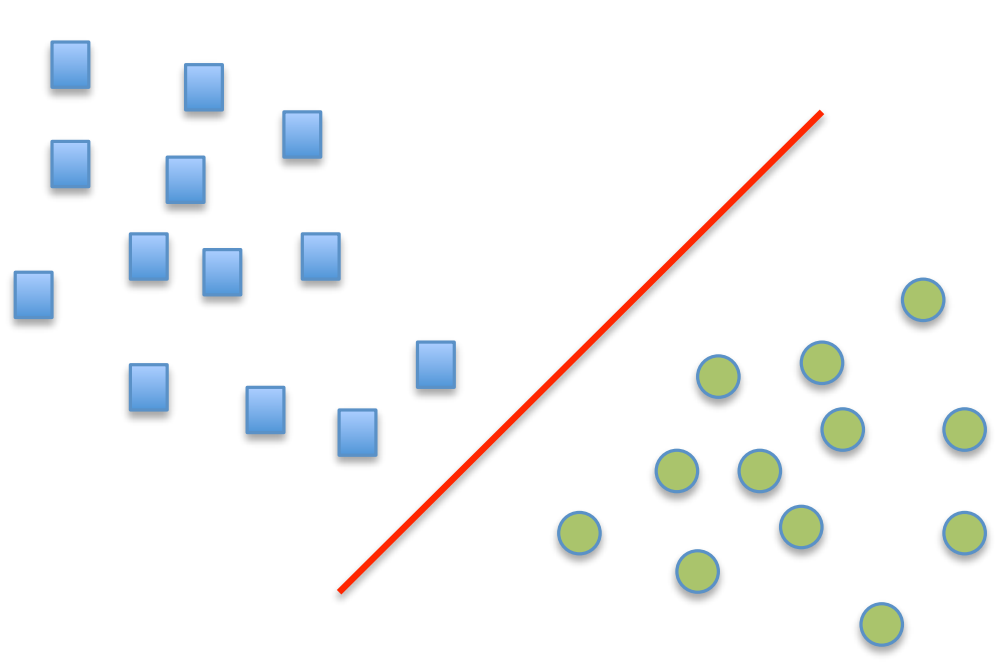
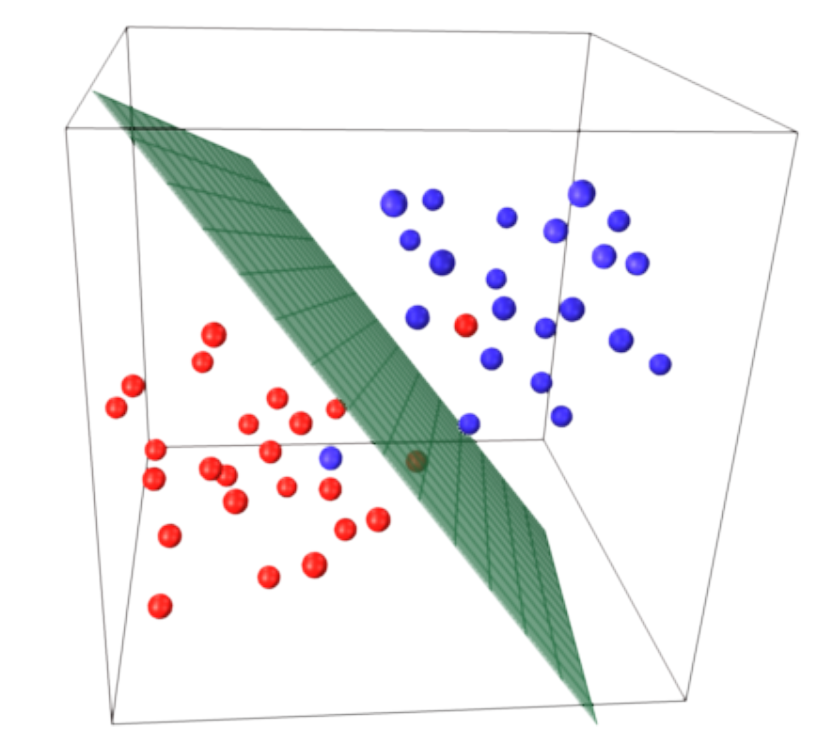
Classification 2D et 3D.
2.1 Régression Linéaire
La régression linéaire est utilisée pour estimer une variable cible $y$ à partir de variables prédictives $x$ à l’aide d’un modèle linéaire.
2.1.1 Modèle de Régression Linéaire
Soit $\mathbf{X}$ une matrice de dimensions $N \times D$ représentant nos caractéristiques pour $N$ exemples et $D$ caractéristiques. La relation entre $\mathbf{X}$ et $\mathbf{y}$ est modélisée par $\mathbf{y} = \mathbf{X} \mathbf{w} + \mathbf{b}$, où :
- $\mathbf{w}$ est un vecteur de poids de longueur $D$.
- $\mathbf{b}$ est le biais.
2.1.2 Fonction de Perte en Régression Linéaire
La fonction de perte pour la régression linéaire est la somme des moindres carrés (ou somme des erreurs quadratiques) :
\[L(\mathbf{w}, \mathbf{b}) = \frac{1}{2N} \left \| \mathbf{y} - \mathbf{X}\mathbf{w} - \mathbf{b} \right \|^2\]2.2 Adaptation à la Classification par les Moindres Carrés
Dans la classification, on utilise la régression linéaire pour estimer les étiquettes de classe dans un contexte binaire.
- Étiquettes de Classe : $\mathbf{t}$ (valeurs de -1 ou 1 pour une classification binaire).
- La fonction de perte devient :
2.2.1 Composante Biais et Matrice Augmentée
Pour incorporer le biais, on ajoute une colonne de uns à gauche de $\mathbf{X}$, créant une matrice augmentée $\tilde{\mathbf{X}}$ de dimensions $N \times (D+1)$.
\[\tilde{\mathbf{X}} = \begin{bmatrix} 1 & x_{1}^T \\ 1 & x_{2}^T \\ \vdots & \vdots \\ 1 & x_{N}^T \\ \end{bmatrix}\]2.2.3 Calcul des Poids Optimaux
En minimisant la fonction de perte par rapport à $\mathbf{w}$ et $\mathbf{b}$, on dérive une solution analytique pour les poids optimaux $\tilde{\mathbf{w}}$ :
\[\tilde{\mathbf{w}} = (\tilde{\mathbf{X}}^T \tilde{\mathbf{X}})^{-1} \tilde{\mathbf{X}}^T \mathbf{t}\]Cette solution est obtenue à l’aide de la pseudo-inverse pour résoudre le système linéaire et fournit les poids optimaux pour la classification des moindres carrés dans un contexte binaire.
2.3 Classification des Moindres Carrés pour plusieurs classes
En utilisant la méthode des moindres carrés pour la classification, on peut l’adapter pour gérer des problèmes multi-classes.
2.3.1 Modèle pour plusieurs classes
Pour chaque classe $C_k$, un modèle linéaire distinct est utilisé :
\[y_k(\mathbf{x}) = \mathbf{w}_k^T \mathbf{x} + w_{k0}\]- $k = 1, \dots, K$ représente les différentes classes.
- $\mathbf{w}_k$ est un vecteur de poids pour la classe $k$ avec une dimension égale à celle des caractéristiques plus le biais.
- $w_{k0}$ est le terme de biais pour la classe $k$.
2.3.2 Vecteur de sortie pour toutes les classes
Regroupons ces modèles en utilisant une notation vectorielle : \(\mathbf{y}(\mathbf{x}) = \mathbf{W}^T \mathbf{x}\)
- $\mathbf{W}$ est une matrice de taille $(D+1) \times K$ où chaque colonne représente les poids pour une classe spécifique.
- $\mathbf{x}$ est le vecteur d’entrée augmenté avec une composante pour le biais.
2.3.3 Fonction de Perte
En utilisant un ensemble de données d’entraînement ${ \mathbf{x}_n, \mathbf{t}_n }$ où $n = 1, \dots, N$ et $\mathbf{t}_n$ est le vecteur cible pour la $n$-ème observation, la fonction de perte peut être définie comme suit :
\[L(\mathbf{W}) = \frac{1}{2N} \| \mathbf{T} - \mathbf{X}\mathbf{W} \|^2\]- $\mathbf{T}$ est une matrice de dimensions $N \times K$ contenant les vecteurs cibles pour chaque exemple d’entraînement.
- $\mathbf{X}$ est une matrice augmentée de taille $N \times (D+1)$ représentant les caractéristiques d’entrée augmentées pour chaque exemple.
2.3.4 Calcul des Poids Optimaux
Pour obtenir les poids optimaux $\mathbf{W}$, on minimise la fonction de perte par rapport à $\mathbf{W}$. La solution est donnée par :
\[\mathbf{W} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{T}\]2.4 Seuil de Décision
2.4.1 Classification Binaire
Pour convertir les prédictions continues en une prédiction binaire, un seuil de décision est choisi. Si la prédiction $\hat{y}(\mathbf{x})$ dépasse ce seuil, on classe l’observation dans la catégorie positive ($1$) ; sinon, elle est classée dans la catégorie négative ($0$). Cela peut être exprimé comme :
\[\hat{t}(x) = \begin{cases} 1 & \text{si } \hat{y}(x) > seuil \\ 0 & \text{sinon} \end{cases}\]2.4.2 Classification multi-classe :
Pour la classification multi-classe, chaque classe possède son propre modèle. La décision est prise en comparant les prédictions de chaque modèle pour attribuer une observation $\mathbf{x}$ à une classe spécifique.
Comparaison des Prédictions : Les prédictions pour chaque classe sont calculées à l’aide des modèles correspondants. La classe prédite pour l’observation $\mathbf{x}$ est celle ayant la prédiction la plus élevée. Cela peut être formulé comme :
\[\hat{t}(x) = \underset{k}{\arg \max} \; \hat{y}_{k}(x)\]où $\hat{y}_k(x)$ représente la prédiction pour la classe $k$.
2.5 Classification Non Binaire
À partir de la section 2.3, on comprend que la méthode de classification des moindres carrés peut être étendue pour traiter des problèmes de classification impliquant plus de deux classes. Pour ce faire, diverses stratégies peuvent être adoptées. Par exemple, les approches One-vs-Rest (OvR) ou One-vs-One (OvO) peuvent être utilisées pour élargir la portée de la classification des moindres carrés.
- OvR (One-vs-Rest) : $K$ modèles sont entraînés, un pour chaque classe par rapport à toutes les autres classes.
- OvO (One-vs-One) : $\frac{K(K-1)}{2}$ modèles binaires sont entraînés pour chaque paire de classes.
2.6 Fonction de perte
On peut appliquer différente fonctions de perte dans des contextes différents selon la manière dont on veut évaluer et pénaliser les erreurs du modèle. Ces fonctions de perte sont utilisées pour mesurer la performance des classificateurs en évaluant la différence entre les prédictions du modèle $(y(x))$ et les vraies étiquettes ($t$).
-
Perte de zéro/une : Cette fonction évalue la perte en fonction de la prédiction par rapport à la vraie étiquette. Elle attribue une perte de 0 lorsque la prédiction est correcte $(y(x) = t)$ et une perte de $1$ lorsqu’il y a une prédiction incorrecte $(y(x) \neq t)$.
\[L_{0-1}(y(x), t) = \begin{cases} 0 & \text{si } y(x) = t \\ 1 & \text{si } y(x) \neq t \end{cases}\] -
Perte binaire asymétrique : Cette perte est utilisée lorsqu’il y a un déséquilibre entre les classes. Elle attribue des poids différents aux erreurs en fonction de la prédiction et de la vraie étiquette. Si $y(x) = 1$ et $t = 0$, la perte est $\alpha$. Si $y(x) = 0$ et $t = 1$, la perte est $\beta$. Pour une prédiction correcte $(y(x) = t)$, la perte est nulle.
\[L_{ABL}(y(x), t) = \begin{cases} \alpha & \text{si } y(x) = 1 \land t = 0 \\ \beta & \text{si } y(x) = 0 \land t = 1 \\ 0 & \text{si } y(x) = t \end{cases}\] -
Perte quadratique : Cette fonction mesure la perte en prenant le carré de la différence entre la prédiction et la vraie étiquette. Elle est souvent utilisée dans la régression et attribue une pénalité plus importante aux erreurs importantes.
\[L_{\text{squared}}(y(x), t) = (t - y(x))^2\] -
Erreur absolue : Cette perte mesure simplement la différence absolue entre la prédiction et la vraie étiquette, ignorant la direction de l’erreur.
\[L_{\text{absolute}}(y(x), t) = |t - y(x)|\]
2.7 Évaluation du modèle
2.7.1 Matrice de Confusion
La matrice de confusion est une matrice $2 \times 2$ (pour une classification binaire) ou $K \times K$ (pour une classification multi-classe) où $K$ est le nombre de classes. Pour une classification binaire, elle est représentée comme suit :
\[\text{Matrice de Confusion} = \begin{bmatrix} VP & FP \\ FN & VN \\ \end{bmatrix}\]2.7.2 Précision et Rappel
La précision en classification mesure l’exactitude des prédictions positives du modèle par rapport à l’ensemble des prédictions positives, tandis que le rappel évalue la capacité du modèle à identifier correctement tous les éléments positifs par rapport à l’ensemble des éléments positifs réels.
La précision et le rappel sont calculés comme suit :
\[\text{Précision} = \frac{VP}{VP + FP} = \frac{VP}{\text{toutes les prédiction}}\] \[\text{Rappel} = \frac{VP}{VP + FN}\]où :
- VP : Vrais Positifs
- FP : Faux Positifs
- FN : Faux Négatifs
Le F1 score est une mesure combinée de la précision et du rappel, représentée par la formule \(F1 = \frac{2 \times \text{Précision} \times \text{Rappel}}{\text{Précision} + \text{Rappel}}\) Cette mesure harmonique donne un équilibre entre la précision et le rappel en calculant la moyenne pondérée des deux. Un F1 score élevé indique à la fois une précision élevée et un rappel élevé, ce qui est bénéfique pour évaluer les performances globales d’un modèle de classification.
2.7.3 Courbe ROC
La courbe ROC est tracée en utilisant le Taux de Vrais Positifs (TPR) et le Taux de Faux Positifs (FPR) : \(\text{TPR} = \frac{VP}{VP + FN}\)
\[\text{FPR} = \frac{FP}{FP + VN}\]2.7.4 Cross-Validation
La validation croisée est une technique pour évaluer la performance d’un modèle en utilisant des sous-ensembles différents des données disponibles. Cela permet d’estimer la capacité du modèle à généraliser de nouvelles données.
2.8 Limitations
La linéarité de la méthode des moindres carrés limite sa capacité à capturer des relations non linéaires entre les caractéristiques et les étiquettes de classe, ce qui peut être problématique pour des modèles plus complexes.
La méthode des moindres carrés manque aussi de robustesse face aux données aberrantes en plus du fait qu’elle peut être inappropriée pour des distributions non gaussiennes. D’autres méthodes, comme la régression logistique, offrent des solutions plus adaptées à ces problèmes.
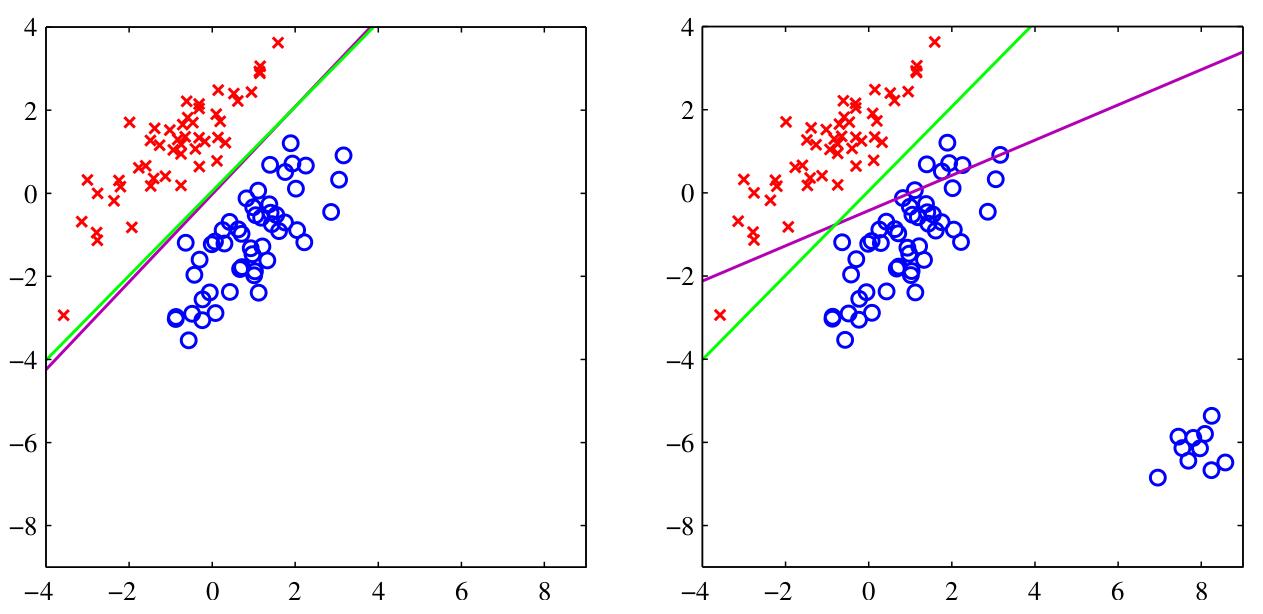
En comparaison avec la classification par régression logistique (couleur vert), il est observable que la régression par la méthode des moindres carrés (couleur magenta) est plus sensible aux valeurs aberrantes. Les moindres carrés peuvent être davantage influencés par les valeurs extrêmes ou atypiques présentes dans les données d’apprentissage.
Références
- Pattern Recognition And Machine Learning, Christopher M. BishopChristopher M. Bishop
- CSC 411: Lecture 03: Linear Classification, Richard Zemel, Raquel Urtasun and Sanja Fidler, University of Toronto
- CSC 411: Lecture 07: Multiclass Classification, Richard Zemel, Raquel Urtasun and Sanja Fidler, University of Toronto
- Derivation of Least Squares Regressor and Classifier, Diego Unzueta
- notesonai